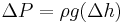Pascal's law

In the physical sciences, Pascal's law or the Principle of transmission of fluid-pressure states that "pressure exerted anywhere in a confined incompressible fluid is transmitted equally in all directions throughout the fluid such that the pressure ratio (initial difference) remains the same."^[1] The law was established by French mathematician Blaise Pascal.^[2]

where

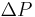is the hydrostatic pressure (given in pascals in the SI system), or the difference in pressure at two points within a fluid column, due to the weight of the fluid;

ρ is the fluid density (in kilograms per cubic meter in the SI system);

g is acceleration due to gravity (normally using the sea level acceleration due to Earth's gravity in metres per second squared);

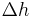is the height of fluid above the point of measurement, or the difference in elevation between the two points within the fluid column (in metres in SI).

The intuitive explanation of this formula is that the change in pressure between two elevations is due to the weight of the fluid between the elevations.

Note that the variation with height does not depend on any additional pressures. Therefore Pascal's law can be interpreted as saying that any change in pressure applied at any given point of the fluid is transmitted undiminished throughout the fluid.

Equation: (P₁)(V₁) = (P₂)(V₂)

Applications

• The siphon
• The underlying principle of the hydraulic jack and hydraulic press
• Force amplification in the braking system of most motor vehicles.
• Used in artesian wells, water towers, and dams.
• Scuba divers must understand this principle. At a depth of 10 meters under water, pressure is twice the atmospheric pressure at sea level, and increases by about 100 kPa for each increase of 10 m depth.^[2]

Also see

• Pascal (unit)
• Fluid statics
• Pascal's contributions to the physical sciences

References